Growing up in a small country, I assumed the whole world used metric grid map coordinates. I mean, why would anyone bother with those tedious latitudes and longitudes when you could have your location defined by something as neat as NS539555?
The tidy, militaristic Ordnance Survey came up with the National Grid reference system, where large grid squares were given letters, and the rest of the reference was given numerically. Wikipedia gives a better graphical explanation than I could:
During WW2, the UK war office extended this system across most of Europe. Since most European countries didn’t use exactly the same Transverse Mercator projection as the UK did, a number of existing mapping systems were pressed into use, but using the same interleaved alphanumeric format as the OS grid reference.
The reference site for these systems is Thierry Arsicaud’s excellent Notes on the “Modified British System” used on the European Theatre of Operations during the WWII. Thierry, however, wasn’t trying to use these historical map references in a GIS, so his work needs a little massage to get to be used with QGIS.
In this example, I’m going to concentrate on the South Italy zone, as that’s where I was asked to look at some war diaries from 1943. The system is similar to the OS grid, but the main difference is that the major grid reference is often given in lower case. So RN in OSGB would most often be denoted rN in the Modified British system. Both would refer to a 100 km square at (700, 700) km from the origin. (The exceedingly nitpicky might point out that RN is never used in the UK as it’s somewhere in the Atlantic, west of Ireland. To them, I say: Well, bless your heart …)
The key to both the OSGB grid and the Modified British system is a 2500 × 2500 km square, split into 25 500 km squares, and given a letter, a … z with i excluded:
Each letter encodes both an easting and a northing; so r is (500000, 500000). About the easiest way to unpack this encoding is through a simple string lookup:
result = SEARCH(letter, "VWXYZQRSTULMNOPFGHJKABCDE")-1 easting = result MOD 5 northing = INT(result / 5)
where SEARCH is a function which returns the position of a letter in a string (so SEARCH(“V”, “VWXYZ…”) returns 1).
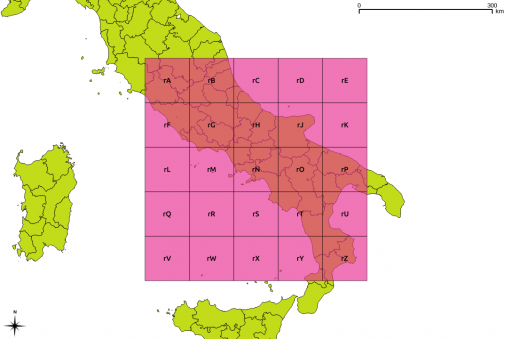
When applied as per the GSGS South Italy system, you get something like this:
These major grid squares are in turn split into 25 minor squares of 100 km side:
Or overlaid on a map:
For grid references of higher precision, a series of numbers is appended. There should always be an even count of these numbers, for reasons which should become clear soon. Here is the rC square, split into 10 km references:
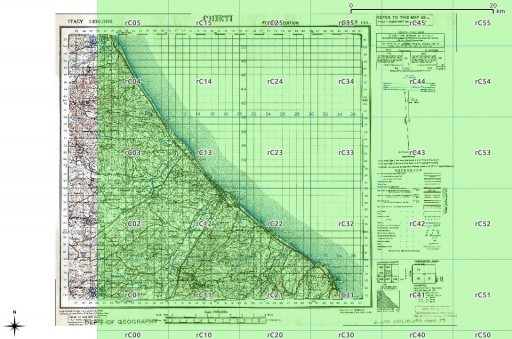
These two digit references are about the shortest/least precise you might ever see. Overlaid on an appropriate sheet from the McMaster archive WWII Topographic Map Series (which are CC BY-NC; for which, many thanks), you get:
The actual projection details are given on each map:
We can turn this into a PROJ.4 definition:
Projection - Lambert Conical Orthomorphic → +proj=lcc
Ellipsoid: Bessel 1841 → +ellps=bessel
False Easting : 700000 → +x_0=700000
False Northing : 600000 → +y_0=600000
Central Meridian : 14.0° → +lon_0=14
Central Parallel : 39.5° → +lat_0=39.5 +lat_1=39.5
Scale Factor : 0.99906 → +k_0=0.99906
(other proj.4 terms) +units=m +no_defs
or in one line,
+proj=lcc +lat_0=39.5 +lat_1=39.5 +lon_0=14 +k_0=0.99906 +x_0=700000 +y_0=600000 +ellps=bessel +units=m +no_defs
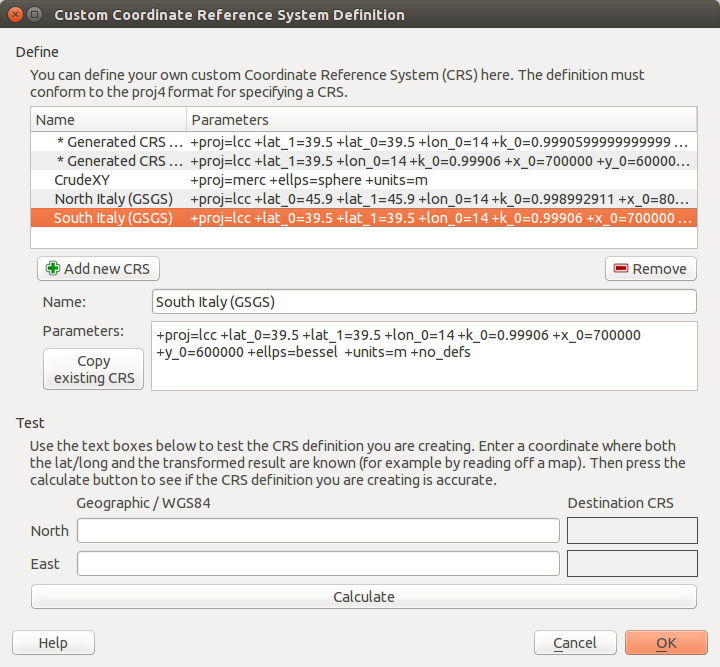
In QGIS, you can plug those values into the Custom CRS manager, and you will be able to work in these antiquated coordinate systems with ease:
I haven’t yet quite managed to work out some of the other GSGS coordinate systems. My work on North Italy is a stubborn 100 km off true, for no well-defined reason. I haven’t managed to work out unpicking alphanumeric grid references into geometries automatically, either. These will come later.
Finally, some of the coordinates you might see might not meet these specifications. In the limited survey I’ve done, I’ve noted:
- references with the major grid missing, so rCxy… was written as Cxy….
- references to ‘MR’ (map reference), with no alphanumeric part, such as MR 322142 (from here), which would be more correctly given as rC322142.
Huge thanks to Thierry Arsicaud, both for the great reference website, and also for the e-mail correspondence helping explain the parameters for the GSGS Italy South system. Props too to the Geographic Information Systems Stack Exchange folks for help with working out the proj.4 settings.



 The antipodes get plotted underneath, and everything looks messed up. I may have to take my question to
The antipodes get plotted underneath, and everything looks messed up. I may have to take my question to 

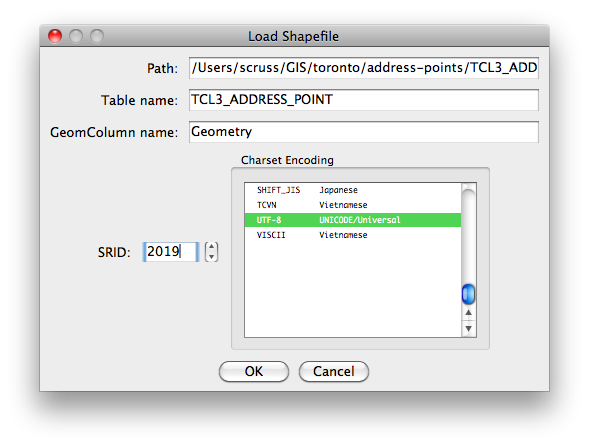 This might take a while, as there are over 500,000 points in this data set.
This might take a while, as there are over 500,000 points in this data set.