Growing up in a small country, I assumed the whole world used metric grid map coordinates. I mean, why would anyone bother with those tedious latitudes and longitudes when you could have your location defined by something as neat as NS539555?
The tidy, militaristic Ordnance Survey came up with the National Grid reference system, where large grid squares were given letters, and the rest of the reference was given numerically. Wikipedia gives a better graphical explanation than I could:
During WW2, the UK war office extended this system across most of Europe. Since most European countries didn’t use exactly the same Transverse Mercator projection as the UK did, a number of existing mapping systems were pressed into use, but using the same interleaved alphanumeric format as the OS grid reference.
The reference site for these systems is Thierry Arsicaud’s excellent Notes on the “Modified British System” used on the European Theatre of Operations during the WWII. Thierry, however, wasn’t trying to use these historical map references in a GIS, so his work needs a little massage to get to be used with QGIS.
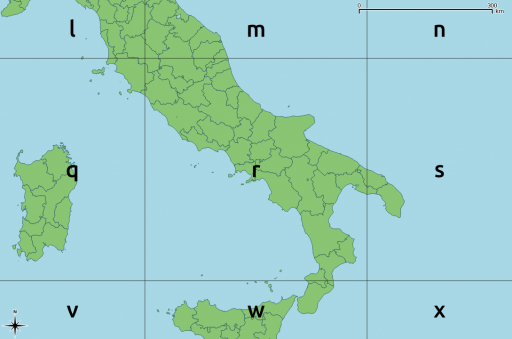
In this example, I’m going to concentrate on the South Italy zone, as that’s where I was asked to look at some war diaries from 1943. The system is similar to the OS grid, but the main difference is that the major grid reference is often given in lower case. So RN in OSGB would most often be denoted rN in the Modified British system. Both would refer to a 100 km square at (700, 700) km from the origin. (The exceedingly nitpicky might point out that RN is never used in the UK as it’s somewhere in the Atlantic, west of Ireland. To them, I say: Well, bless your heart …)
The key to both the OSGB grid and the Modified British system is a 2500 × 2500 km square, split into 25 500 km squares, and given a letter, a … z with i excluded:
Each letter encodes both an easting and a northing; so r is (500000, 500000). About the easiest way to unpack this encoding is through a simple string lookup:
result = SEARCH(letter, "VWXYZQRSTULMNOPFGHJKABCDE")-1 easting = result MOD 5 northing = INT(result / 5)
where SEARCH is a function which returns the position of a letter in a string (so SEARCH(“V”, “VWXYZ…”) returns 1).
When applied as per the GSGS South Italy system, you get something like this:
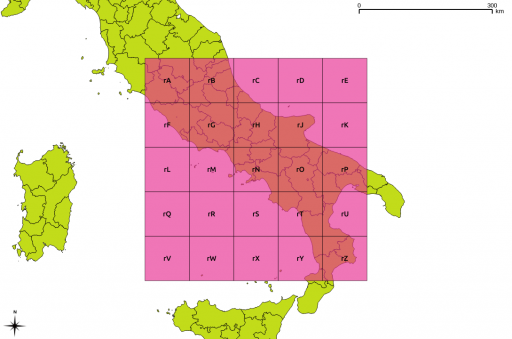
These major grid squares are in turn split into 25 minor squares of 100 km side:
Or overlaid on a map:
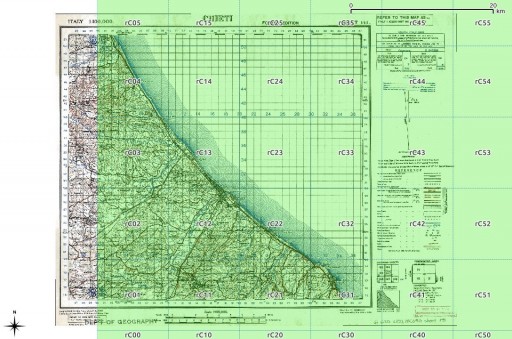
For grid references of higher precision, a series of numbers is appended. There should always be an even count of these numbers, for reasons which should become clear soon. Here is the rC square, split into 10 km references:
These two digit references are about the shortest/least precise you might ever see. Overlaid on an appropriate sheet from the McMaster archive WWII Topographic Map Series (which are CC BY-NC; for which, many thanks), you get:
The actual projection details are given on each map:
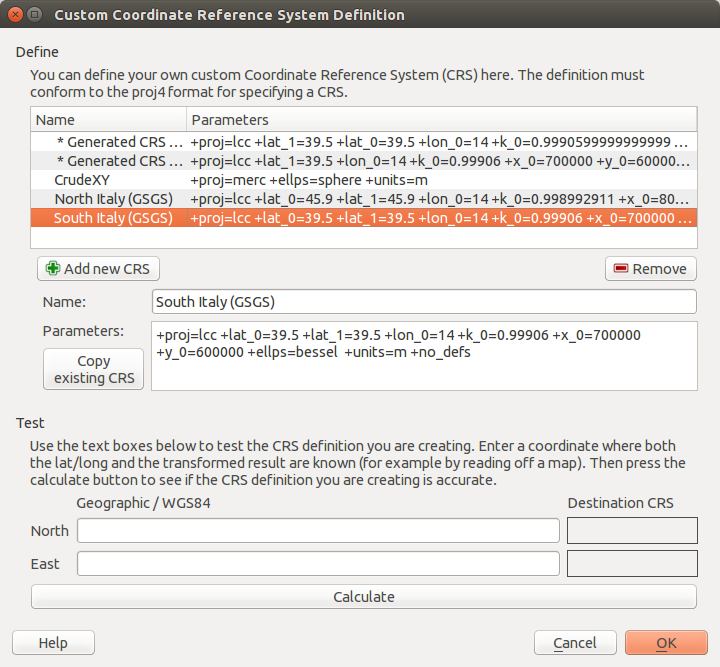
We can turn this into a PROJ.4 definition:
Projection - Lambert Conical Orthomorphic → +proj=lcc
Ellipsoid: Bessel 1841 → +ellps=bessel
False Easting : 700000 → +x_0=700000
False Northing : 600000 → +y_0=600000
Central Meridian : 14.0° → +lon_0=14
Central Parallel : 39.5° → +lat_0=39.5 +lat_1=39.5
Scale Factor : 0.99906 → +k_0=0.99906
(other proj.4 terms) +units=m +no_defs
or in one line,
+proj=lcc +lat_0=39.5 +lat_1=39.5 +lon_0=14 +k_0=0.99906 +x_0=700000 +y_0=600000 +ellps=bessel +units=m +no_defs
In QGIS, you can plug those values into the Custom CRS manager, and you will be able to work in these antiquated coordinate systems with ease:
I haven’t yet quite managed to work out some of the other GSGS coordinate systems. My work on North Italy is a stubborn 100 km off true, for no well-defined reason. I haven’t managed to work out unpicking alphanumeric grid references into geometries automatically, either. These will come later.
Finally, some of the coordinates you might see might not meet these specifications. In the limited survey I’ve done, I’ve noted:
- references with the major grid missing, so rCxy… was written as Cxy….
- references to ‘MR’ (map reference), with no alphanumeric part, such as MR 322142 (from here), which would be more correctly given as rC322142.
Huge thanks to Thierry Arsicaud, both for the great reference website, and also for the e-mail correspondence helping explain the parameters for the GSGS Italy South system. Props too to the Geographic Information Systems Stack Exchange folks for help with working out the proj.4 settings.

20 replies on “Some notes on the wartime “Modified British” map coordinate systems”
I am also trying to do something skmilar with the maps in Romania, but I am getting a weird 3km shift to the east. Can we maybe talk by email?
Sorin
Further to Sorin’s comment, this approximates to the Danube Zone coordinates, as far as I can tell:
Thank you for the helpful information. Unfortunately working on the “Italy South” grid with GQIS, as well as ArcMap, I get a residual error of about 300/400 meters. Any suggestion on how to solve this problem?
Not any immediate suggestions, sorry. Which map sheet(s) are you working from?
Thank you Russell, I am working on the classic GSGS maps (1:100K, but even 1:25k, and some 1:10k) The curious thing is that I get a non-negligible offset even converting the coordinates by the converter at Thierry Arsicaud’s website. I suppose there should be a way to calibrate the projection parameters in order to compensate the offset. But I am a novice with QGIS. What do you think about?
I managed to figure out a really good transformation for the Netherlands, both in ArcMap and QGIS. I can tell you it was not easy. Figuring out the projection params alone does not suffice. You also need to know how the map projection relates to the projection you are currently using.
I can try to help if you let me know the specific map sheets you’re trying to work from
Well, if it were easy, I wouldn’t have had to write this page!
As long as you know how to convert from a historical map projection to WGS84, you can let QGIS manage the conversion to your preferred display coordinate system. Usually …
I am trying to georeference in Arcgis this map https://www.loc.gov/resource/g8352bm.gct00176/?sp=17 of Djibouti-Somaliland using the parameters shown in the sheet and the coordinates in degrees, minutes and seconds of the corners of the map.
Every attempt I make to transform these coordinates gives me a different result …
Could you help me convert them as accurately as possible to WGS84?
Thanks
I got “close enough” with setting the CRS to (in proj format)
+proj=tmerc +ellps=clrk80 +lon_0=42.5 +lat_0=0.0 +x_0=400000 +y_0=4500000 +units=m +no_defsas stated on the map. I could then georeference from the the metre grid.
This map’s based on 90 year old colonial survey data, so may not be very relevant
For the Netherlands I located plus 100 corresponding points in current projection and projection on the GSGS-map and used those to calculate Helmert Transformation params. From there I georeference all the GGGS maps in the system specified on the map and use the Helmert Transformation to either transform On-the-fly or reproject(/warp) the map into the current projection. Currently I georeferenced plus 400 GSGS maps of the Netherlands with scale 1:25.000, using most of the 1000 meter grid intersections . The end goal is to cover the whole of the Netherlands. Still have a few maps to go but well on my way. Arcmap and Qgis use different ways to specify custom projections. Consult the help for a how-to.
Good to know. 100 points might be a little overkill per map, but whatever works. I usually do 8-10 and knock off the two points with the highest residuals.
I used plus 100 points scattered over the Netherlands, for all the Dutch maps. So I can reproject all 428 maps together with only one transformation for the entire country. Why so many points? The datum was intentionally skewed in several areas. And the maps vary in accuracy. Even the parts of the maps vary in accuracy.
ah right – I thought you meant 100 points *per map sheet*.
At least the Dutch maps didn’t get the sarcastic notes that other countries got from the GSGS cartographers.
Thanks Scruss and Joey for your help.
I have configured the CRS in Qgis, georeferencing the map as you indicate and then reprojecting it. Everything’s fine.
I understand that the precision of the result is variable due to the origin of the data, but they are what I have …
The question that remains for me now is to know if this way of doing it is more precise than using the geographical coordinates that appear on the map and which are the “originals” collected in the version of the maps from the 30s (https: // www .loc.gov / resource / g8352bm.gct00177 /? sp = 2).
Regarding the transformation used, I have tried the different options (linear, Helmert …), observing that the results vary. Any recommendation in this case?
Thanks again and sorry if my questions are very basic … and my English very bad
Greetings
I wrote an intro to georeferencing some time ago that might help:
http://glaikit.org/2011/03/27/image-georeferencing-with-qgis/
Use the red metre grid and enter coordinates as metres in the georeferencer. There are a lot more intersection points to go on that just the DDMMSS at the corners,
Probably best to use Helmert transformation for these maps, as they mostly just need scaling and rotation. The Residual display you get with QGIS is handy, as it shows you which points are the least accurate.
You can use Raster → Warp to convert to 4326, which works better than expected since this map isn’t too far north of the equator.
I have not been a serious QGIS user for nearly a decade. I’m probably not the person to ask.
@maffs
As I see it there’s three routes you can take.
Route 1 is the easiest. Georeference the map directly in WGS84 using corresponding points on your gsgs-map and the map in WGS84. In QGIS Georeferencer set your target CRS to WGS84, set your from-to points, choose your transformation type and transform. In Arcmap check if your CRS is WGS84 in the data frame properties, open georeferencing toolbar, set your from-to points, choose a transformation type and apply. Choosing a transformation type is the trickiest part because the different types have different results. What’s best depends on your input and desired accuracy. Checking the output is easier in Arcmap because you can georeference on-the-fly. Meaning you can directly see the result. Don’t forget to apply though.
Route 2 is a bit harder because it involves setting a transformation, if one is available in either QGIS or Arcmap. First you georeference your gsgs-map in the CRS specified on the gsgs-map. Then set your target map CRS to WGS84 and set a transformation. Consult the EPSG database you can find online for an appropriate transformation. Both Qgis and Arcmap will propose one for you that you can then set. It’s always good to check what’s proposed. Consult either QGIS or Arcmap help for a how to on setting transformations.
Route 3 is the hardest and is the same as route 2 apart from the added step where you have to make a custom transformation. Both calculating the transformation and setting a custom transformation are a bit cumbersome. In both QGIS and Arcmap. I don’t recommend this as it took me quite a while to do this for the Dutch maps. In hindsight it was fun but it did give me a few headaches.
Thanks again for your comments.
@scruss, I appreciate what you have taught me and I think you are a person to ask.
@joey, I’ll try a mix of options 1 and 2 that you propose to georeference the maps … I hope to do it well.
My plan is:
-georeference the map with the CRS specified in the sheet according to the scruss contribution, using different points of the “red” mesh
-transform to WGS84. I have tried different types of transformations and except the linear one, I don’t see a big difference between Helmert, polynominal or spline, which are the ones that best fit (within the error)
I haven’t been able to find the proper parameters for a custom transformation setup for arcgis (Create custom geographic transformation> method), so I’ll settle for this.
Thanks for the help.
@maffs
There’s two types of transformations. The first is from unreferenced scan to you GIS’s Coordinate Reference System (CRS). The second is to get from that CRS to the WGS84 CRS.
First georeference your gsgs-map in the CRS specified on the map itself using the Georeferencer with an appropriate type of Transformation (linear, polynomial, Helmert or other).
Second transform your freshly georeferenced map into WGS84 or any other CRS you wish.
You can bypass the second by directly georeferencing your map in WGS84 using corresponding points in your gsgs-map and WGS84 map. You probably won’t be able to use the maps grid coordinates then. Because these coordinates are likely not the same as the WGS84 coordinates in the geographic area concerned. Here you’ll need a custom transformation when your GIS does not have one for you.
Specifying your gsgs-maps CRS as target system for the georeferencer does not get it in WGS84.
@maffs
Possibly found a geographic transformation for the Djibouti map. Have to do some checks first.